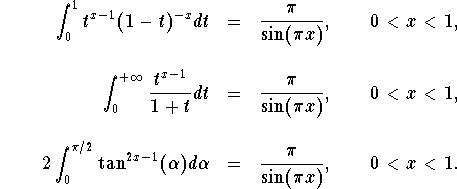Many important functions in applied sciences are defined via improper
integrals. Maybe the most famous among them is the
Gamma
Function. This is why we thought it would be a good idea to have a
page on this function with its basic properties. You may consult any
library for more information on this function.
Historically the search for a function generalizing the factorial
expression for the natural numbers was on. In dealing with this
problem one will come upon the well-known formula
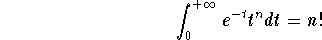
A very quick approach to this problem suggests to replace
n by
xin the improper integral to generate the function
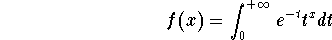
Clearly this definition requires a close look in order to determine
the domain of
f(
x). The only possible bad points are 0 and
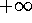
. Let us look at the point 0. Since
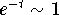
when
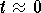
, then we have
when
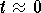
. The p-test implies that we have convergence
around 0 if and only if -
x < 1 (or equivalently
x >-1). On the
other hand, it is quite easy to show that the improper integral is
convergent at
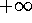
regardless of the value of
x. So the
domain of
f(
x) is
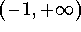
. If we like to have
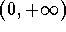
as a domain, we will need to translate the x-axis to
get the new function
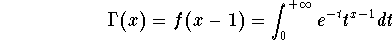
which explains somehow the
awkward term
x-1 in the power of
t. Now the domain of
this new function (called the
Gamma Function) is
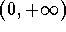
. The above formula is also known as
Euler's second integral(if you wonder about Euler's first integral, it is coming a little
later).
Basic Properties of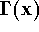 
First,
from the remarks above we have
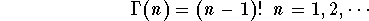
One of the most important formulas satisfied by
the Gamma function is
for any
x > 0.
In order to show this formula from the definition of
, we will use the following identity
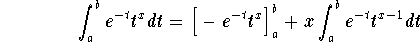
(this is just an integration by parts). If we let
a goe to 0 and
b goe to
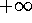
, we get the desired identity.
In particular, we get
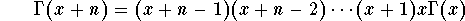
for any
x > 0 and any integer
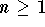
. This formula makes it
possible for the function
to be extended to
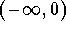
(except for the negative integers). In particular, it is enough to know
on the interval (0,1] to know the function for any
x > 0.
Note that since
we get
. Combined with the above identity, we get what we
expected before :
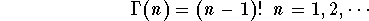
A careful analysis of the Gamma function (especially
if we notice that
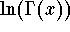
is a convex
function) yields the inequality
or equivalently
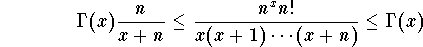
for every
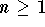
and
x >0. If we let
n goe to
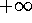
, we
obtain the identity
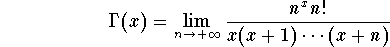
Note that this formula identifies the Gamma function in a unique
fashion.
Weierstrass identity. A simple algebraic
manipulation gives
Knowing that the sequence
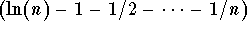
converges to the constant -
C, where
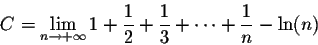
is the Euler's constant. We get
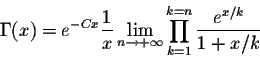
or
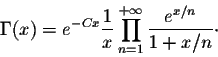
The logarithmic derivative of the Gamma
function: Since
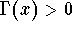
for any
x >0, we can take the logarithm of the
above expression to get
If we take the derivative we get
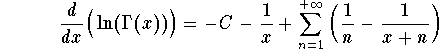
or
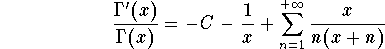
In fact, one can differentiate the Gamma function infinitely often.
In "analysis" language we say that
is of
-class. Below you will find the graph of the Gamma
function.
The Beta FunctionEuler's first integral or the Beta function: In
studying the Gamma function, Euler discovered another function, called
the
Beta function, which is closely related to
.
Indeed, consider the function
It is defined for two variables
x and
y. This is an
improper integral of Type I, where the potential bad points are 0 and
1. First we split the integral and write
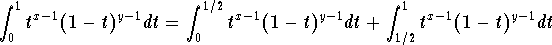
When
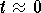
, we have
and when
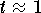
, we have
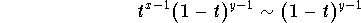
So we have convergence if and only if
x > 0 and
y >0 (this is done
via the p-test). Therefore the domain of
B(
x,
y) is
x > 0 and
y>0. Note that we have
Let
a and
b such that
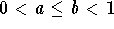
, we have (via an integration
by parts)
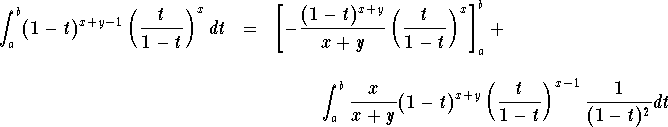
If we let
a goe to 0 and
b goe to 1, we will get
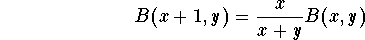
Using the properties of the Gamma function, we get
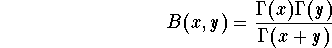
or
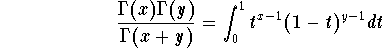
In particular, if we let
x=
y = 1/2, we get
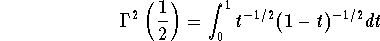
If we set
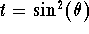
or equivalently
, then the technique of substitution implies
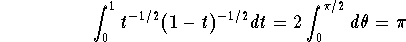
Hence we have
or
Using this formula, we can now easily calculate the value of
.
Other Important Formulas: The following formulas are given without detailed proofs. We hope
they will be of some interest.
Asymptotic behavior of the Gamma function when
x is large: We have
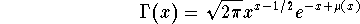
where
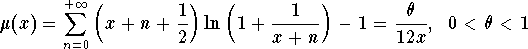
If we take,
x=
n, we get after multiplying by
n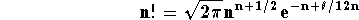 
This is a well known result, called
Stirling's formula. So for large
n, we
have
The connection with 
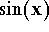: For any
x >
0, we have
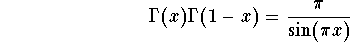
which implies
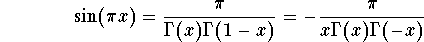
Using the Weierstrass product formula (for
and
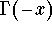
), we get
If we use the Beta function (
B(
x,
y)), we get the following formulas:
موضوع: Gamma Function 
الإثنين نوفمبر 16, 2009 4:15 am
